222 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

题解

本题可以先用共通方法：求解二叉树的节点个数来做。

二叉树节点个数递归法

递归参数，递归终止条件和递归单层逻辑

递归参数： root， 返回值 当前树节点个数

递归终止条件， root === null, 返回0，空节点是0个

递归的单层逻辑

const leftTreeCount = countNodes(root.left)
const rightTreeCount = countNodes(root.right)

return leftTreeCount + rightTreeCount + 1 //当然root 节点是1

整体算法

var countNodes = function(root) {
    if(!root) {
        return 0
    }
    const leftTreeCount = countNodes(root.left)
    const rightTreeCount = countNodes(root.right)
    return leftTreeCount + rightTreeCount + 1
}

二叉树节点个数迭代法

这里利用模版的迭代法

var countNodes = function(root) {
    const stack = []
    let result = 0
    if(!root) {
        return result
    }
    stack.push(root)

    while(stack.length) {
        const current = stack.pop()

        if(current) {
            if(current.right) {
                stack.push(current.right)
            }
            if(current.left) {
                stack.push(current.left)
            }
            //处理节点,这里是先序遍历
            stack.push(current)
            stack.push(null)
        } else {
            //处理节点
            const actual = stack.pop()
            //console.log('ff', actual.val)
            result++
        }
    }
    return result
}

完全二叉树的节点个数解法

我们要利用好完全二叉树的特性，

完全二叉树特性：除了最底层外，其他层都是满的，如果最底层没满，都是靠左的位置

那么假设完全二叉树是满二叉树，我们可以直接求解， 满二叉树的个数是 2^n-1 (n 是高度)，但是如果不满的话怎么办，我们可以分解。

利用随想录的一张图来解释怎么利用完全二叉树的特性：

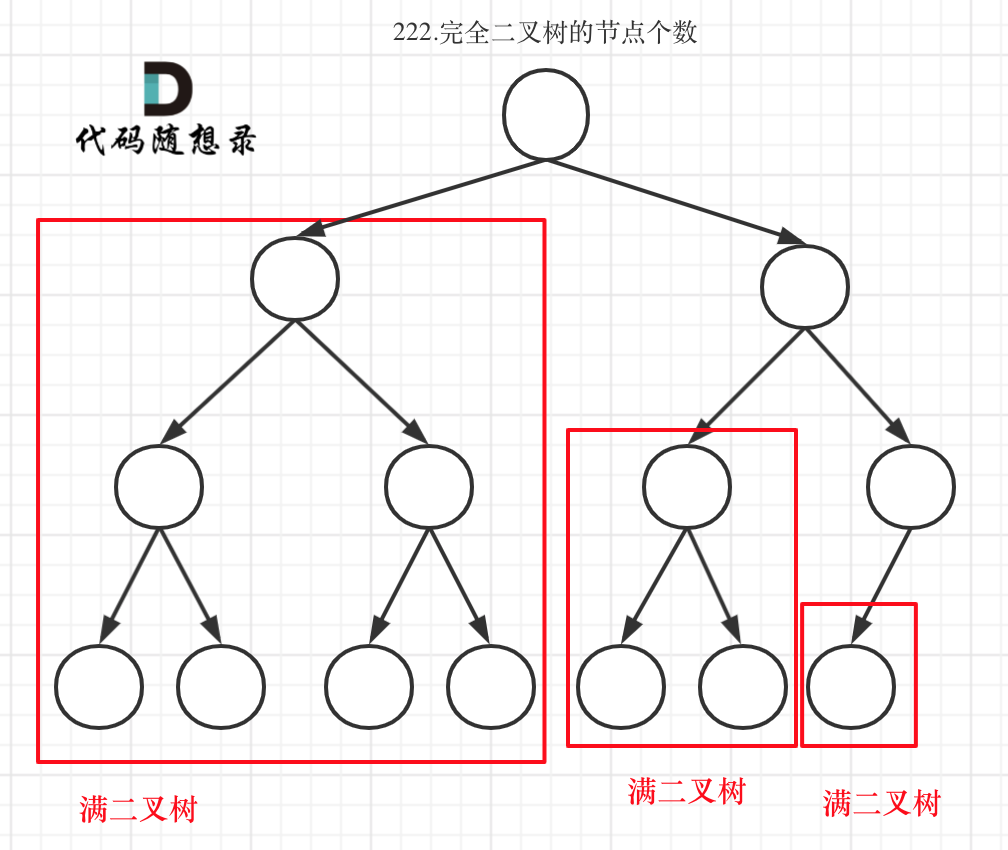
每一层都可以是满二叉树。

下面的问题就变成了怎么判断一棵树是不是满二叉树呢？在完全二叉树这个条件下，我们可以利用最左边的深度和最右边的深度判断。

如果深度一样，那么一定是满二叉树，如果深度不一样，一定不是。

递归三部曲

递归的参数和返回值 参数root，返回值节点个数

递归的终止条件，如果左右子树是满二叉树，可以直接求解，返回

if(!root) return 0
let leftDepth = 0
const rootLeft = root
while(rootLeft) {
    leftDepth++
    rootLeft = rootLeft.left
}
let rightDepth = 0
const rootRight = root
while(rootRight) {
    rightDepth++
    rootRight = rootRight.right
}

//如果相同，直接求解
if(leftDepth === rightDepth) {
    return Math.pow(2, n) - 1
}

递归的单层逻辑

const leftCount = countNodes(root.left)
const rightCount = countNodes(root.right)
return leftCount + right + 1

所以整体解法

var countNodes = function(root) {
    if(!root) {
        return 0
    }
    let leftDepth = 0
    let rootLeft = root
    while(rootLeft) {
        leftDepth++
        rootLeft = rootLeft.left
    }
    let rightDepth = 0
    let rootRight = root
    while(rootRight) {
        rightDepth++
        rootRight = rootRight.right
    }

    //如果相同，直接求解
    if(leftDepth === rightDepth) {
        return Math.pow(2, rightDepth) - 1
    }

    const leftTreeCount = countNodes(root.left)
    const rightTreeCount = countNodes(root.right)

    return leftTreeCount + rightTreeCount + 1
}